Categorical EDA
Mengxiao Luan, Yuzhe Hu
2023-12-07
Carrying out some descriptive and exploratory analysis based on cleaned data sets.
We conduct some exploratory analysis from three main aspects:
regarding general distribution:
- net worth of wealth(billions of dollars)
- approach of becoming a billionaire(self-made or not)
- wealth status(increasing, decreasing, stable or returning)
regarding demographic information:
- age
- gender
- country(country of citizenship, country of residence)
regarding economic development:
- industry
- industry GDP
library(tidyverse)
library(readxl)
library(janitor)
library(forcats)
library(plotly)
library(ggpubr)knitr::opts_chunk$set(
echo = TRUE,
warning = FALSE,
message = FALSE,
fig.width = 8,
fig.height = 6,
out.width = "90%"
)
options(
ggplot2.continuous.colour = "viridis",
ggplot2.continuous.fill = "viridis"
)
scale_colour_discrete = scale_colour_viridis_d
scale_fill_discrete = scale_fill_viridis_d
theme_set(
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5),
text = element_text(family = "Helvetica")) +
theme(legend.position = "right"))# import data
bil_2010_2023 =
read_csv("../data/billionaire_gdp.csv") |>
select(-starts_with("region")) |>
drop_na()
bil_gdp = read_csv("../data/billionaire_gdp_indus_usa.csv") |>
select(-(age:wealth_status)) |>
drop_na()Focus on data collected in 2023
Have a quick look at the data.
# filter data
bil_2023 =
bil_2010_2023 |>
filter(year == 2023)
# describe data
bil_2023 |>
skimr::skim()| Name | bil_2023 |
| Number of rows | 2338 |
| Number of columns | 11 |
| _______________________ | |
| Column type frequency: | |
| character | 7 |
| logical | 1 |
| numeric | 3 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| full_name | 0 | 1 | 5 | 38 | 0 | 2336 | 0 |
| gender | 0 | 1 | 4 | 6 | 0 | 2 | 0 |
| country_of_citizenship | 0 | 1 | 4 | 20 | 0 | 75 | 0 |
| country_of_residence | 0 | 1 | 4 | 24 | 0 | 74 | 0 |
| city_of_residence | 0 | 1 | 3 | 24 | 0 | 699 | 0 |
| wealth_status | 0 | 1 | 9 | 16 | 0 | 4 | 0 |
| industries | 0 | 1 | 6 | 26 | 0 | 18 | 0 |
Variable type: logical
| skim_variable | n_missing | complete_rate | mean | count |
|---|---|---|---|---|
| self_made | 0 | 1 | 0.71 | TRU: 1662, FAL: 676 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1 | 2023.00 | 0.00 | 2023 | 2023.0 | 2023.00 | 2023.0 | 2023 | ▁▁▇▁▁ |
| net_worth | 0 | 1 | 4.85 | 10.32 | 1 | 1.5 | 2.45 | 4.5 | 211 | ▇▁▁▁▁ |
| age | 0 | 1 | 65.51 | 13.07 | 26 | 56.0 | 65.00 | 75.0 | 101 | ▁▅▇▆▁ |
General Distributions
Distribution of Wealth
right-skewed wealth data
age increases in each wealth group
more males than females in each wealth group
First depict the overall wealth distribution of the billionaires.
# overall distribution
wealth_distribution_1 =
bil_2023 |>
ggplot(aes(x = net_worth)) +
geom_histogram() +
labs(x = "Net wealth(billion dollars)",
y = "Count")
wealth_distribution_2 =
bil_2023 |>
ggplot(aes(x = net_worth)) +
geom_density() +
labs(x = "Net wealth(billion dollars)",
y = "Density")
ggarrange(wealth_distribution_1, wealth_distribution_2,
labels = c("A", "B"), ncol = 1, nrow = 2) |>
annotate_figure(
top = text_grob("Overall wealth distribution of billionaires in 2023"))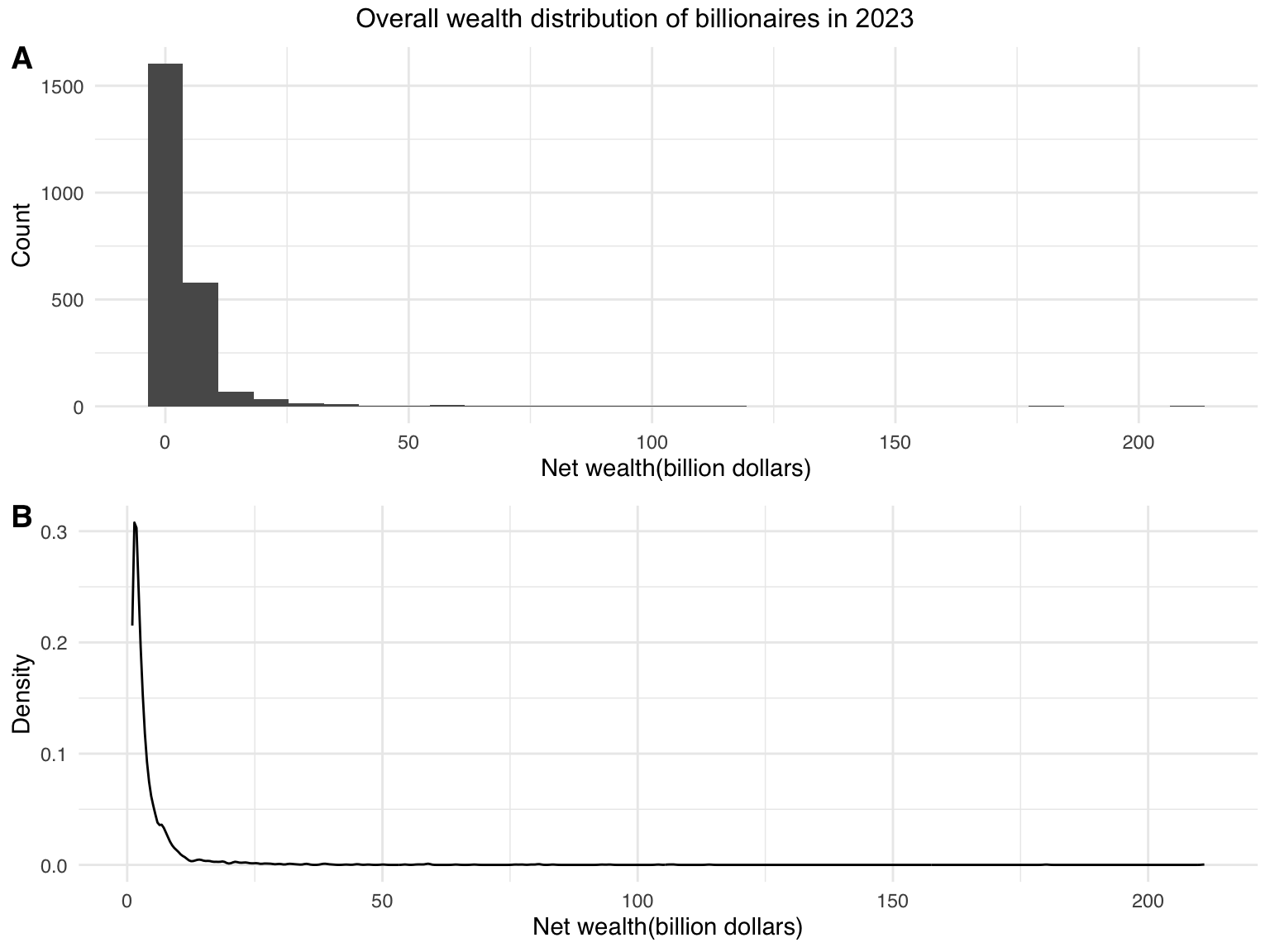
It can be seen from the plots that the wealth distribution in 2023 is right-skewed, with outliers lying on the right side of the axis.
Further transformation may be required for detailed tests and regression model fitting. Try a relatively simple transformation to better visualize the distribution shown above.
boxcox_result =
MASS::boxcox(lm(net_worth ~ 1, data = bil_2023), plotit = FALSE) |>
as.data.frame()
boxcox_plot =
ggplot(boxcox_result, aes(x = x, y = y)) +
geom_line() +
labs(title = "Box-cox plot for transformation parameter selection",
x = plotly::TeX("$\\lambda$"),
y = "Box-cox transformation of response variable")
ggplotly(boxcox_plot) |> config(mathjax = "cdn")wealth_distribution_3 =
bil_2023 |>
ggplot(aes(x = net_worth^(-0.5))) +
geom_histogram() +
labs(x = "Net wealth(transformed)",
y = "Count")
wealth_distribution_4 =
bil_2023 |>
ggplot(aes(x = net_worth^(-0.5))) +
geom_density() +
labs(x = "Net wealth(transformed)",
y = "Density")
ggarrange(wealth_distribution_3, wealth_distribution_4,
labels = c("A", "B"), ncol = 1, nrow = 2) |>
annotate_figure(
top = text_grob("Transformed wealth distribution of billionaires in 2023"))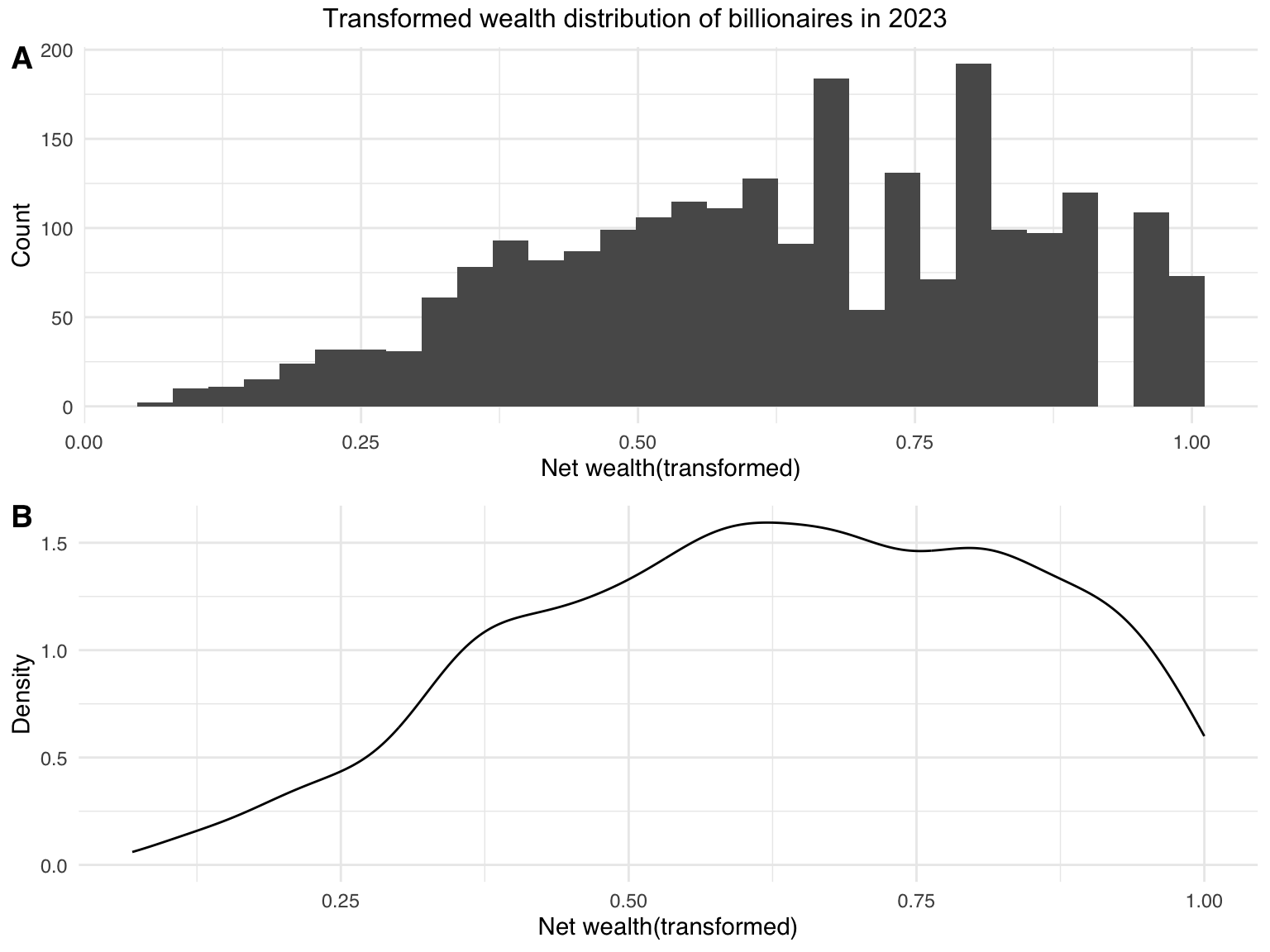
The transformed distribution shows better normality compared with orignial data, yet more precise methods should be applied in further analysis, with the specific procedure depending on the analytic goal.
Divide the whole population into several wealth groups to see detailed distribution in different groups.
# division
billionairs_wealth =
bil_2023 |>
mutate(
net_worth =
case_when(
net_worth <= 5 ~ "<=5",
net_worth > 5 & net_worth <= 10 ~ "5~10",
net_worth > 10 & net_worth <= 100 ~ "10~100",
net_worth > 100 ~ ">100"
)) |>
mutate(
net_worth =
forcats::fct_relevel(
net_worth, c("<=5", "5~10", "10~100", ">100")
))
# description
billionairs_wealth |>
group_by(net_worth) |>
summarize(N = n()) |>
mutate(Proportion = N/sum(N)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| net_worth | N | Proportion |
|---|---|---|
| <=5 | 1834 | 0.7844311 |
| 5~10 | 329 | 0.1407186 |
| 10~100 | 169 | 0.0722840 |
| >100 | 6 | 0.0025663 |
# visualization
## number of people
billionairs_wealth |>
count(net_worth) |>
plot_ly(x = ~net_worth, y = ~n, color = ~net_worth,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires in different wealth groups",
xaxis = list(title = "Net wealth(billion dollars)"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## age
billionairs_wealth |>
plot_ly(y = ~age, color = ~net_worth, type = "box", colors = "viridis") |>
layout(title = "Age distribution of different wealth groups",
xaxis = list(title = "Net wealth(billion dollars)"),
yaxis = list(title = "Age of billionaires"),
font = list(family = "Helvetica"))## gender
wealth_gender_distribution =
billionairs_wealth |>
ggplot(aes(x = net_worth, fill = gender)) +
geom_histogram(stat = "count", position = "dodge", binwidth = 15) +
labs(title = "Gender distribution of different wealth groups",
xaxis = list(title = "Net wealth(billion dollars)"),
yaxis = list(title = "Number of billionaires"))
ggplotly(wealth_gender_distribution)The table and plots show that the majority of billionaires possess a net wealth no more than 5 billion dollars.
The number of people decreaeses while the average age increases in each group as the wealth goes up. There are more male billionaires than female in each group, and the group with largest net wealth consists of all males.
Distribution of Approach
more self-made billionaires
no significant difference in wealth
Use the approach(self-made or not) as the factor to view the distribution.
# description
bil_2023 |>
group_by(self_made) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
mutate(Proportion = N/sum(N)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| self_made | mean_wealth | N | Proportion |
|---|---|---|---|
| FALSE | 5.396154 | 676 | 0.289136 |
| TRUE | 4.628460 | 1662 | 0.710864 |
# visualization
## number of people
bil_2023 |>
count(self_made) |>
plot_ly(x = ~self_made, y =~n, color = ~self_made,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires: self-made or not",
xaxis = list(title = "Approach: self-made or not"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
bil_2023 |>
plot_ly(y = ~net_worth, color = ~self_made,
type = "box", colors = "viridis") |>
layout(title = "Net wealth of self-made or not billionaires",
xaxis = list(title = "Approach: self-made or not"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))The proportion of self-made billionaires is way larger, yet there is no significant difference in the wealth distribution plot of the two groups.
Distribution of Status
most decreased
larger wealth in increased group
Similarly, explore the underlying distribution of entrepreneur and inherited billionaires.
# description
bil_2023 |>
group_by(wealth_status) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
mutate(Proportion = N/sum(N)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| wealth_status | mean_wealth | N | Proportion |
|---|---|---|---|
| Decreased | 4.753820 | 1191 | 0.5094098 |
| Increased | 6.090942 | 828 | 0.3541488 |
| Remained Even | 2.096094 | 256 | 0.1094953 |
| Returned to List | 1.565079 | 63 | 0.0269461 |
# visualization
## number of people
bil_2023 |>
count(wealth_status) |>
plot_ly(x = ~wealth_status, y =~n, color = ~wealth_status,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires with different wealth status",
xaxis = list(title = "Wealth status"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
bil_2023 |>
plot_ly(y = ~net_worth, color = ~wealth_status,
type = "box", colors = "viridis") |>
layout(title = "Net wealth of billionaires with different wealth status",
xaxis = list(title = "Wealth status"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))The outliers in decreased and increased groups may indicate that billionaires with large amount of wealth tend to fluctuate in respect of net wealth.
Demographic Distributions
Distribution of Age
relatively symmetric age data
wealth increases in each age group
Similar to the processing of wealth information, divide the population into four age groups to investigate the number and wealth distribution in details.
# overall distribution
age_distribution_1 =
bil_2023 |>
ggplot(aes(x = age)) +
geom_histogram() +
labs(x = "Age",
y = "Count")
age_distribution_2 =
bil_2023 |>
ggplot(aes(x = age)) +
geom_density() +
labs(x = "Age",
y = "Density")
ggarrange(age_distribution_1, age_distribution_2,
labels = c("A", "B"), ncol = 1, nrow = 2) |>
annotate_figure(
top = text_grob("Overall age distribution of billionaires in 2023"))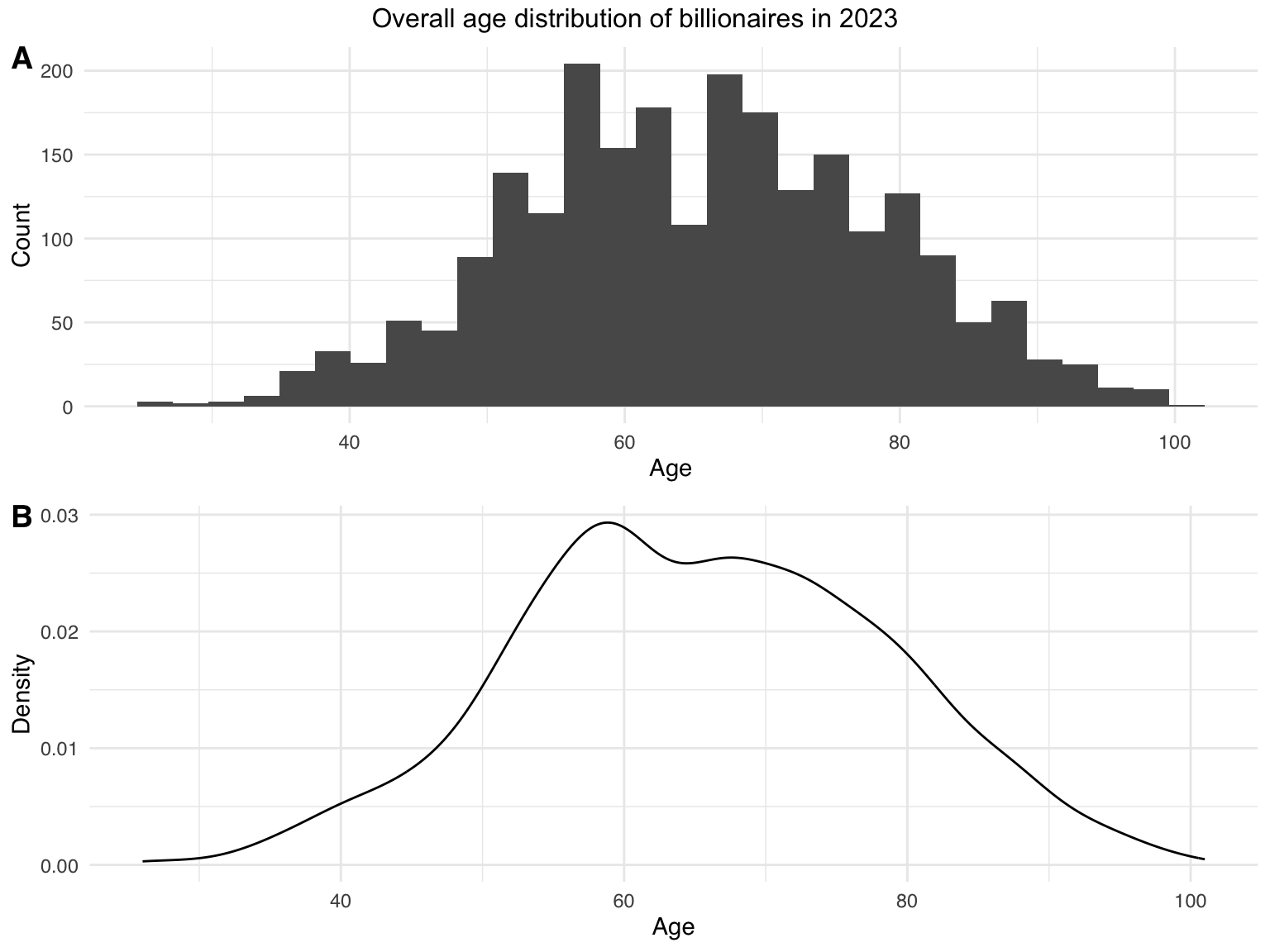
# division
billionairs_age =
bil_2023 |>
mutate(
age =
case_when(
age <= 55 ~ "<=55",
age > 55 & age <= 65 ~ "55~65",
age > 65 & age <= 75 ~ "65~75",
age > 75 ~ ">75")) |>
mutate(
age =
forcats::fct_relevel(
age, c("<=55", "55~65", "65~75", ">75")))
# description
billionairs_age |>
group_by(age) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
mutate(Proportion = N/sum(N)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| age | mean_wealth | N | Proportion |
|---|---|---|---|
| <=55 | 4.262289 | 533 | 0.2279726 |
| 55~65 | 4.300932 | 644 | 0.2754491 |
| 65~75 | 5.088576 | 604 | 0.2583405 |
| >75 | 5.790305 | 557 | 0.2382378 |
# visualization
## number of people
billionairs_age |>
count(age) |>
plot_ly(x = ~age, y = ~n, color = ~age,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires in different age groups",
xaxis = list(title = "Age"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
billionairs_age |>
plot_ly(y = ~net_worth, color = ~age, type = "box", colors = "viridis") |>
layout(title = "Net wealth of different age groups",
xaxis = list(title = "Age"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))age_distribution_3 =
billionairs_age |>
ggplot(aes(x = age, y = net_worth)) +
geom_violin(aes(fill = age), alpha = 0.5) +
labs(title = "Net wealth of different age groups",
x = "Age of billionaires",
y = "Net wealth(billion dollars)")
ggplotly(age_distribution_3)The overall age distribution is much more symmetric, resulting in a relatively evenly distributed number in the four groups. Though not very significant, the average net wealth tends to increase as the age of the group increases.
Distribution of Gender
more male billionaires than female
similar wealth in gender groups
Compare the proportion and average wealth possession of billionaires with different genders.
# description
bil_2023 |>
group_by(gender) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
mutate(Proportion = N/sum(N)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| gender | mean_wealth | N | Proportion |
|---|---|---|---|
| Female | 4.936704 | 267 | 0.1142002 |
| Male | 4.839305 | 2071 | 0.8857998 |
# visualization
## number of people
bil_2023 |>
count(gender) |>
plot_ly(x = ~gender, y = ~n, color = ~gender,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires of different genders",
xaxis = list(title = "Gender"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
bil_2023 |>
plot_ly(y = ~net_worth, color = ~gender, type = "box", colors = "viridis") |>
layout(title = "Net wealth of different gender groups",
xaxis = list(title = "Gender"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))gender_distribution =
bil_2023 |>
ggplot(aes(x = gender, y = net_worth)) +
geom_violin(aes(fill = gender), alpha = 0.5) +
labs(title = "Net wealth of different gender groups",
x = "Gender of billionaires",
y = "Net wealth(billion dollars)")
ggplotly(gender_distribution)There is a way larger proportion of male billionaires compared with female. Despite the more extreme outliers in male group, the average net wealth of the two groups are similar to each other.
We can also plot using both age and gender as factors to see the distribution of net wealth in each subgroups.
age_gender_distribution =
billionairs_age |>
ggplot(aes(x = age, y = net_worth)) +
geom_violin(aes(fill = age)) +
facet_grid(gender~.) +
labs(title = "Net wealth of different genders and age groups",
x = "Age of billionaires",
y = "Net wealth(billion dollars)")
ggplotly(age_gender_distribution)The panels separated by gender exhibit similar distribution patterns to the combined ones above, with more data points as well as outliers in the group of male, and no siginificant difference in different age groups.
Distribution of Country
overlaps in counrty of citizenship and residence
potential difference in wealth in billionaires of each country
The countries of citizenship and residence are quite scattered in distribution. Filter the top 10 countries with most billionaires to see the net wealth distribution in each country.
# description
bil_2023 |>
group_by(country_of_citizenship) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
arrange(desc(N)) |>
slice(1:10) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| country_of_citizenship | mean_wealth | N |
|---|---|---|
| United States | 6.465620 | 669 |
| China | 3.488403 | 457 |
| India | 4.311348 | 141 |
| Germany | 5.059794 | 97 |
| Russia | 4.814894 | 94 |
| Hong Kong | 4.912903 | 62 |
| Canada | 4.045763 | 59 |
| Brazil | 3.352174 | 46 |
| Italy | 3.654348 | 46 |
| United Kingdom | 4.140909 | 44 |
# visualization
## number of people
bil_2023 |>
count(country_of_citizenship) |>
mutate(country_of_citizenship = fct_reorder(country_of_citizenship, n)) |>
plot_ly(x = ~country_of_citizenship, y = ~n, color = ~country_of_citizenship,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires with different citizenship",
xaxis = list(title = "Country of citizenship"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth of top 10
citizenship =
bil_2023 |>
group_by(country_of_citizenship) |>
summarize(n_obs = n()) |>
arrange(desc(n_obs)) |>
slice(1:10) |>
pull(country_of_citizenship)
bil_2023 |>
filter(country_of_citizenship %in% citizenship) |>
plot_ly(x = ~country_of_citizenship, y = ~net_worth,
color = ~country_of_citizenship, type = "box", colors = "viridis") |>
layout(title = "Net wealth of billionaires with different citizenship",
xaxis = list(title = "Country of citizenship(top 10)"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))# description
bil_2023 |>
group_by(country_of_residence) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
arrange(desc(N)) |>
slice(1:10) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| country_of_residence | mean_wealth | N |
|---|---|---|
| United States | 6.417758 | 687 |
| China | 3.567769 | 484 |
| India | 4.299237 | 131 |
| Germany | 4.883333 | 84 |
| United Kingdom | 4.707895 | 76 |
| Russia | 4.609333 | 75 |
| Switzerland | 4.708696 | 69 |
| Hong Kong | 4.320312 | 64 |
| Italy | 2.964444 | 45 |
| Brazil | 2.490000 | 40 |
# visualization
## number of people
bil_2023 |>
count(country_of_residence) |>
mutate(country_of_residence = fct_reorder(country_of_residence, n)) |>
plot_ly(x = ~country_of_residence, y = ~n, color = ~country_of_residence,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires with different residence",
xaxis = list(title = "Country of residence"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth in top 10
residence =
bil_2023 |>
group_by(country_of_residence) |>
summarize(n_obs = n()) |>
arrange(desc(n_obs)) |>
slice(1:10) |>
pull(country_of_residence)
bil_2023 |>
filter(country_of_residence %in% residence) |>
plot_ly(x = ~country_of_residence, y = ~net_worth,
color = ~country_of_residence, type = "box", colors = "viridis") |>
layout(title = "Net wealth of billionaires with different residence",
xaxis = list(title = "Country of residence(top 10)"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))There are actually many overlaps in the country with most citizenship and residence, which leads to the similarity in the two box plots.
Industry Distribution
different number of billionaires in each industry
potential difference in wealth distribution
To better understand the relationship between the development of industries and the arise of billionaires, describe and visualize the distribution of billionaires in different industry fields.
# description
bil_2023 |>
group_by(industries) |>
summarize(mean_wealth = mean(net_worth),
N = n()) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| industries | mean_wealth | N |
|---|---|---|
| Automotive | 7.864615 | 65 |
| Construction & Engineering | 2.660976 | 41 |
| Diversified | 4.775595 | 168 |
| Energy | 4.807692 | 91 |
| Fashion & Retail | 6.870563 | 231 |
| Finance & Investments | 4.513056 | 337 |
| Food & Beverage | 4.823429 | 175 |
| Gambling & Casinos | 4.820000 | 25 |
| Health care | 3.313889 | 180 |
| Logistics | 4.378125 | 32 |
| Manufacturing | 3.320761 | 289 |
| Media & Entertainment | 5.088889 | 81 |
| Metals & Mining | 6.618462 | 65 |
| Real Estate | 3.503049 | 164 |
| Service | 3.340000 | 50 |
| Sports | 4.259259 | 27 |
| Technology | 6.290690 | 290 |
| Telecom | 6.966667 | 27 |
# visualization
## number of people
bil_2023 |>
count(industries) |>
mutate(industries = fct_reorder(industries, n)) |>
plot_ly(x = ~industries, y = ~n, color = ~industries,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires in different industries",
xaxis = list(title = "Industry field"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
bil_2023 |>
plot_ly(x = ~industries, y = ~net_worth, color = ~industries,
type = "box", colors = "viridis") |>
layout(title = "Net wealth of billionaires in different industries",
xaxis = list(title = "Industry field"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))bil_2023 |>
mutate(industries = fct_reorder(industries, net_worth)) |>
ggplot(aes(y = industries, x = net_worth)) +
geom_violin(aes(fill = industries), alpha = 0.5) +
labs(title = "Net wealth of billionaires in different industries",
x = "Industry field",
y = "Net wealth(billion dollars)")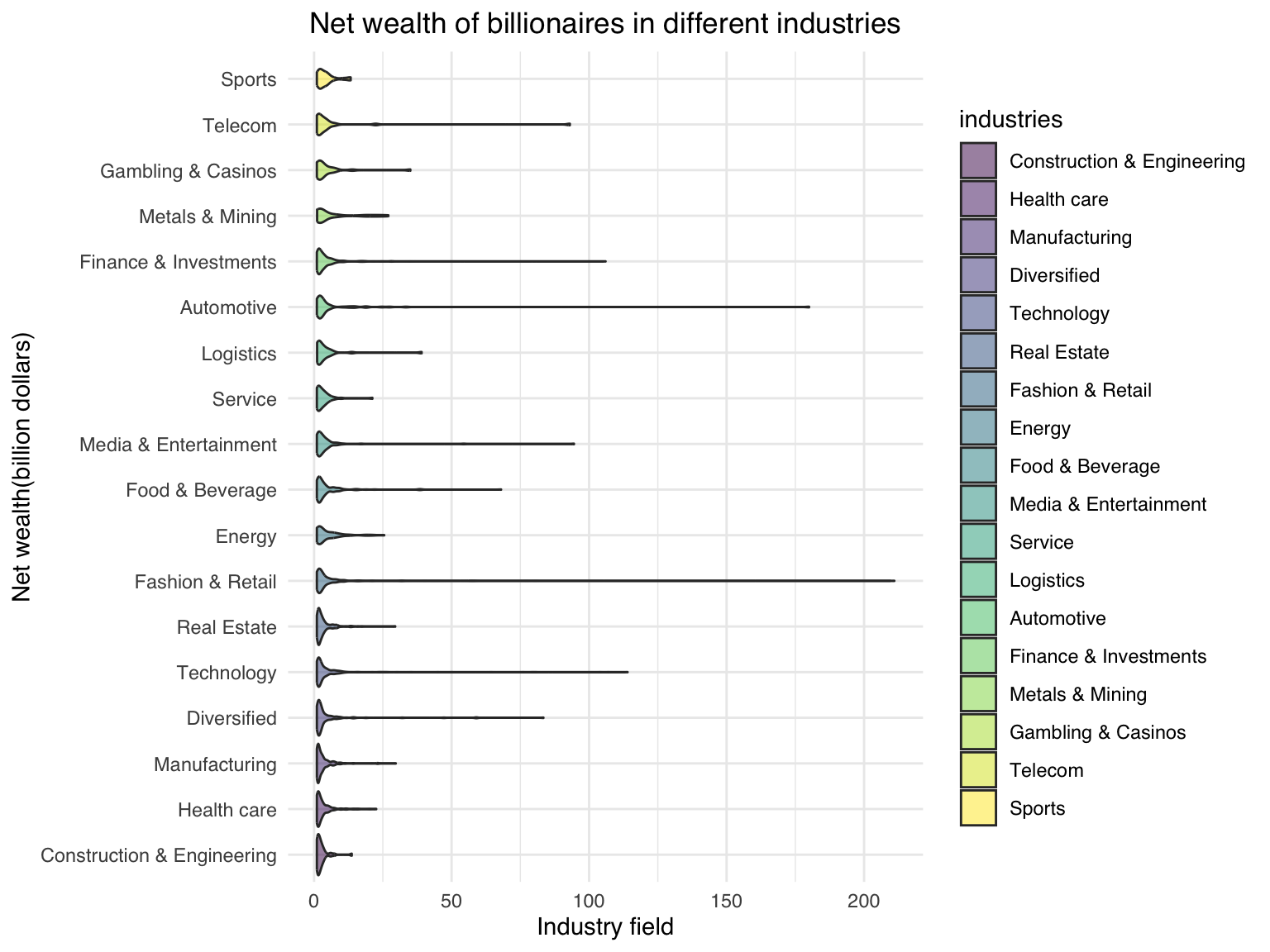
The wealth distributions in different industries look close to each other due to the extreme outliers, which requires further test to verify the potential trends.
Compare data collected in 2013 and 2023
increased number and wealth over time
more male billionaires than female
We can compare some basic distribution between different years as well. Filter the data collected in year 2013 and 2023 to show the change over a decade.
# filter data
bil_2013_2023 =
bil_2010_2023 |>
filter(year == 2013 | year == 2023) |>
mutate(year = as.factor(year))
# description
## overall number and wealth
bil_2013_2023 |>
group_by(year) |>
summarize(N = n(),
mean_wealth = mean(net_worth)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| year | N | mean_wealth |
|---|---|---|
| 2013 | 1134 | 4.156711 |
| 2023 | 2338 | 4.850428 |
## number and wealth grouped by gender
bil_2013_2023 |>
group_by(year, gender) |>
summarize(N = n(),
mean_wealth = mean(net_worth)) |>
knitr::kable() |>
kableExtra::kable_styling(bootstrap_options = c("striped", "hover"))| year | gender | N | mean_wealth |
|---|---|---|---|
| 2013 | Female | 99 | 4.278283 |
| 2013 | Male | 1035 | 4.145082 |
| 2023 | Female | 267 | 4.936704 |
| 2023 | Male | 2071 | 4.839305 |
# visualization
## number of people
year_gender_distribution_1 =
bil_2013_2023 |>
ggplot(aes(x = gender, group = year, fill = year)) +
geom_histogram(stat = "count", position = "dodge") +
labs(title = "Gender distribution: 2013 versus 2023",
x = "Gender of billionaires",
y = "Number of billionaires")
ggplotly(year_gender_distribution_1)## net worth
bil_2013_2023 |>
plot_ly(x = ~year, y = ~net_worth, color = ~year,
type = "box", colors = "viridis") |>
layout(title = "Overall wealth distribution: 2013 versus 2023",
xaxis = list(title = "Year of data collection"),
yaxis = list(title = "Net wealth(billion dollars)"),
font = list(family = "Helvetica"))year_gender_distribution_2 =
bil_2013_2023 |>
ggplot(aes(y = net_worth, x = gender, fill = gender)) +
geom_violin() +
facet_grid(.~year) +
labs(title = "Wealth distribution over gender and year",
x = "Gender of billionaires",
y = "Net wealth(billion dollars)")
ggplotly(year_gender_distribution_2)The total number of billionaires have increased over time, with a larger amount of average net wealth in each group as well. The proportion of male remains dominated, yet further tests are needed before reaching a conclusion.
Switch to GDP data
- combined with GDP distribution
The GDP of different industries may be more relevant to the arise and distribution of billionaires rather than the field type itself. The combination of these data is depicted as below, which only focuses on industry GDP in the US due to the restriction of available data.
# visualization
## number of people
bil_gdp |>
filter(year == 2022) |>
group_by(industries, industry_gdp) |>
summarize(n_obs = n()) |>
mutate(industries = fct_reorder(industries, n_obs),
text_label =
str_c("Industry: ", industries,
"\nIndustry GDP: ", industry_gdp,
"\nNumber of Billionaires: ", n_obs)) |>
plot_ly(x = ~industries, y = ~n_obs, color = ~industries,
mode = "markers", text = ~text_label,
type = "bar", colors = "viridis") |>
layout(title = "Number of billionaires in different industries in USA, 2022",
xaxis = list(title = "Industry field"),
yaxis = list(title = "Number of billionaires"),
font = list(family = "Helvetica"))## net worth
bil_gdp |>
filter(year == 2022) |>
mutate(
text_label =
str_c("Industry: ", industries,
"\nIndustry GDP: ", industry_gdp,
"\nNet Wealth of Billionaire: ", net_worth)) |>
plot_ly(x = ~industries, y = ~net_worth, color = ~industries,
mode = "markers", text = ~text_label,
type = "scatter", colors = "viridis") |>
layout(title = "Net wealth versus industry GDP in USA, 2022",
xaxis = list(title = "Industry(with GDP(trillion dollars))"),
yaxis = list(title = "Net wealth of billionaires(billion dollars)"),
font = list(family = "Helvetica"))bil_gdp |>
filter(year == 2022) |>
mutate(
text_label =
str_c("Industry: ", industries,
"\nIndustry GDP: ", industry_gdp,
"\nNet Wealth of Billionaire: ", net_worth)) |>
plot_ly(x = ~industry_gdp, y = ~net_worth, color = ~industries,
mode = "markers", text = ~text_label,
type = "scatter", colors = "viridis") |>
layout(title = "Net wealth versus industry GDP in USA, 2022",
xaxis = list(title = "Industry GDP(trillion dollars)"),
yaxis = list(title = "Net wealth of billionaires(billion dollars)"),
font = list(family = "Helvetica"))It can be seen from the plot that the number and net wealth of billionaires are quite different in different industries, with largest number and wealth falling in Finance & Investments and Technology, respectively.